1 、研究背景介绍

　　随着社会技术的发展，各行业对产品微小化的需求不断提升， 微细加工技术也得到了广泛关注。微细电火花铣削加工是利用简单电极在数控系统控制下，按一定轨迹作成形运动以获得所需工件形状的加工方法。其依靠电蚀作用蚀除工件材料，因此可用来加工传统加工中难以制作的超硬材料。在复杂三维实体制造过程中，其使用简单形状的管状电极或棒状电极，采用逐层扫掠的方式由二维面叠加而成，省去了复杂的成形电极的制备过程，节约了时间和成本，提高了加工效率，增加了制造柔性[1]，是三维行腔加工的一种有效方法。

　　在铣削加工中，由于使用的管状或棒状电极的截面积远远小于要加工型腔的截面积，所以在电极在长度方向上的损耗量十分巨大，直接影响到加工精度，严重地制约了电火花铣削的实际应用[2]。国内外研究学者在电火花铣削补偿方面做了大量研究。Yu 率先提出了等损耗的概念，并利用这种方法加工出了复杂三维型腔。Bleys 提出了一种联合补偿方法，即将预测补偿和实时补偿相结合，以避免加工过深所带来的误差[3-4]。Bissacco 和Mahardika 等提出了基于放电参数检测的补偿方法，实现了对电极损耗的实时补偿[5-6]。此外，Yan 提出了基于CCD 的图像识别法，比较了在不同的铣削深度和电极旋转与否的情况下电极的损耗情况[7]。大连理工大学又在等损耗的基础上提出了均匀损耗分段补偿方法，基于网格划分的电极损耗补偿方法，以及变分层厚度等方法[8-10]。迟关心提出了采用管状电极进行电火花铣削加工的方法，提高了加工表面修正精度和铣削效率[11]。周勇[12]提出了一种工具电极轴向补偿的方法，并在实验中得到了较好的验证。李翔龙[13]提出了一种基于进化神经网络的电极损耗预测补偿方法，反映出了电火花加工的规律。裴景玉[14-15]针对电火花铣削加工，建立了型腔加工底面轮廓的数学模型， 并提出了微细电火花铣削的定长补偿加工方法，实现了加工的实时补偿，提高了尺寸精度和形状精度。

　　利用定长补偿方法进行电火花铣削加工，再配合电极旋转，电极会逐渐形成稳定的圆锥形[16]。而三维型腔的电火花铣削采用分层加工的方法，每层分两步进行，锥形的特征会导致在第一层加工后型腔底面形成一道道残余凸起组成的不平整面，破坏了定长补偿模型初始加工面为平面的条件。因此如何解决在不平整面上继续采用定长补偿方法进行平

　　面加工就显得尤为关键。本文对电火花铣削加工型腔的一层残余底面形貌进行研究，分别建立了三角形仿真模型和正弦型仿真模型模拟底面轮廓，通过改变相应参数，对型腔一层最佳表面的获取及影响因素进行探讨，得出了相应规律，为后续第二层及整个型腔加工提供了理论参考。

　　 2 、基于锥形电极定长补偿加工方法

　　如图1 所示，在电火花加工中，电极按预定轨迹y=g(x)在工件表面加工，但由于电极在加工过程中存在电极损耗，使实际加工出的底面为H(x)，其中y=G(x)表示工件待加工表面。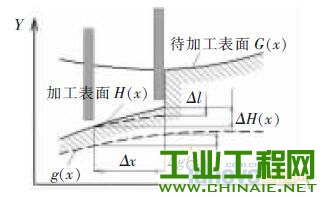

　　定长补偿方法被用来弥补在电加工过程中因电极的损耗引起的底面不平整。如图2 所示，其加工过程可分为3 个部分，分别为电极做垂直于工件表面的打孔加工、水平的铣削加工以及再次垂直于工件表面的补偿加工。HW称为加工中的初始分层厚度，水平运动距离L 称做补偿长度，le称为该方法的补偿精度。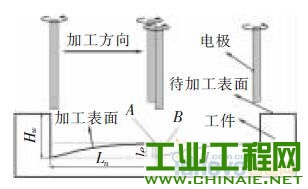

　　3 、基于定长补偿的微细型腔加工方法

　　3.1 型腔第一层加工

　　三维型腔的电火花铣削采用分层加工的方法，用定长补偿法配合旋转， 电极会形成稳定锥形，为减小其对底面波动造成的影响，利用该方法加工型腔第一层分为3 个步骤。如图3a 所示，首先，对加工工件进行预加工处理，即为沿着需加工型腔的最外沿进行一圈加工，这样再进行后续的交替变向加工时就不会出现未加工的残留部分;第二步进行连

　　续变方向交替加工， 以无轨迹重叠的方式进行加工;第三步是将第二步加工残余锯齿面中三角凸起的中心连续线作为铣削加工的加工轨迹。白色的点表示加工起点，黑色的点表示加工终点。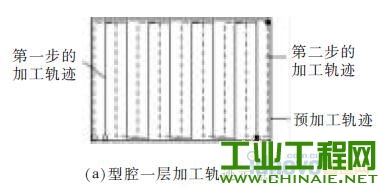

　　图3b 是经两步加工后得到的加工底面显微照片，可看出，原来第一步的加工底部的痕迹仍存在，同时第二步的加工是在第一步的两道相邻的加工轨迹中间进行的。所以原来第一步加工留下的三角形凸起，现在就变成了第二步加工的加工痕迹。

　　3.2 一层残余底面对二层加工影响的仿真研究

　　利用定长补偿方法加工型腔一层后会留下波浪状的加工表面，破坏了定长补偿初始加工表面为平面的模型，因此需对初始加工表面为波浪面的情况下， 上节中提出的铣削策略依旧适用进行验证。为了简化模型，建立了如图4 所示的正弦函数模拟加工表面。α 表示电极端面三角形的底角，d 表示电极直径，HW表示分层厚度，σ 表示放电间隙。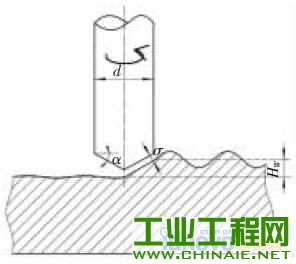

　　基于电火花加工通用的理论模型[17]，结合图1，将工件的待加工表面用方程y=G(x)表示，棒状电极按照y=g(x)的轨迹加工，实际加工出的底面为H(x)。这里拟建立加工非平面的圆锥形电极加工的数学模型。定义待加工的波浪面的中间位置和加工后的小波浪面的中间位置的距离为加工深度HW，并定义这里的深度为带有符号的，其值为负数。

　　仿真的建立基于以下两点假设：

　　(1)加工深度为HW的波浪面形成的锥形电极的角度与加工平面的锥形角度相同，不考虑加工中圆锥形角度的变化。

　　(2)加工后底面的波动很小，远小于待加工面的波动量。

　　基于以上假设及几何分析，采用MATLAB 方法仿真，仿真过程中使用的加工参数见表1。

　　表1 加工参数表

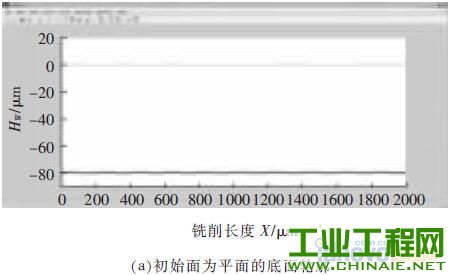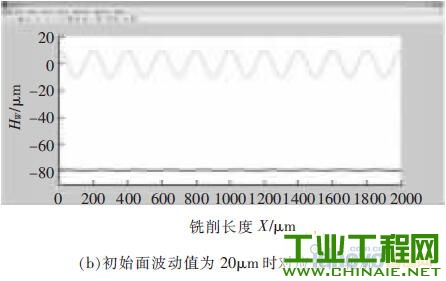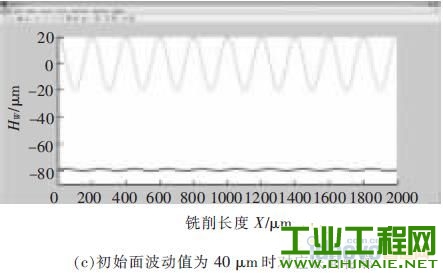　　3.3 获取第二步理想分层厚度的方法

　　由3.2 节仿真结果可得出结论： 上一层加工后形成的波浪面初始表面对下一层继续使用定长补偿方法进行铣削加工型腔底面的几乎不产生影响。这对研究第一层第一步加工后形成的波浪面尤为重要。尽管波浪面作为初始加工表面并不影响接下来多层铣削的底面平整度，但对于波浪面的波动量仍需进一步研究，尽可能使其所形成的底面在深度尺寸及平整度方面达到实验预期。

　　利用定长补偿方法加工型腔，在第一层加工之后会形成如图6a 所示的底面轮廓。传统意义上的最佳表面为不平整表面的两波峰或两波谷之间的距离最小，即图6b 所示①、②、③等3 处面积分别相等。虽然这样的表面减小了几何形状误差，却给定长补偿方法分层厚度的计算和程序的编写带来麻烦。实验中，将一层加工后底面变换成一个统计意义上的平面，此平面的特征为：在一个虚拟的统计平面之上的残切工件体积，与虚拟的统计平面之下的过切工件体积相等，即分层线上下应该满足关系式①与②的面积之和等于③的面积。此时认为该深度为第二步加工的最佳深度值。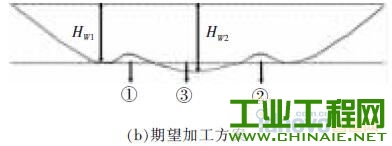

　　如图7 所示，第一步加工后的残余底面为不规则表面，无法通过计算准确获取第二步加工的分层厚度。通过设置辅助线可清晰看出，第一步加工后的残余轮廓线介于三角形和同幅同半周期的正弦曲线之间，并依此得到第一层第二步加工的最佳分层厚度区间。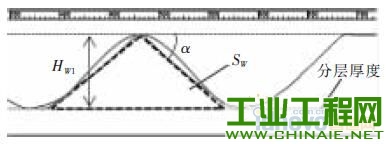

　　 4 、实验及结果

4.1 实验安排

　　通过上节的仿真及分析可知，一层残余底面对二层的加工并无影响，所以能找到第一层第二步的最佳分层厚度是后续加工的关键所在。经计算，在实际加工中，当第一步加工深度为HW1=34.3 μm，即第一步加工补偿长度为L1=60 μm 时， 通过三角形假设和正弦曲线假设得到的第二步最佳分层厚度取值区间为HW2=44~52 μm。为了进步细化区间并提高效率，本实验采用平行加工3 道槽的简化方法模拟型腔加工，实验设备和加工参数见表2 和表3。

　　表2 实验仪器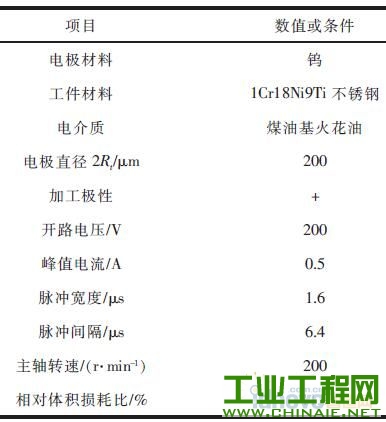

　　4.2 实验结果

　　利用共聚焦显微镜生成的加工截面轮廓见图8。测量时忽略底面轮廓深度的过渡段，直接在稳定阶段对应的部分分为3 个采样点进行测量，在加工长度达到2 mm 时，加工达到稳定段。因此，加工槽上测量点选加工长度为2.5、3、3.5 mm 处分别多次采样进行测量并求取平均值。

　　在不同的采样点处得到分层线上下区域的截面图后， 分别得到分层线上下的两部分区域的面积，利用MATLAB 图像处理方法求取分层线上面区域的面积和与分层线下区域的面积的比值，比值越接近1，则表示此时对应的深度值越接近最佳深度，计算结果见表4。

　　由表4 可看出， 当第二步加工深度为46 μm时，上下区域面积的百分比为86.48 %，最接近100%，受加工机床精度所限，很难再对所分加工区间进行细化，因此认为此时为最佳的加工深度，也即用此深度作为第二步加工时的分层厚度进行铣削;当分层厚度为44 μm 时，上下面积比值大于100 %的值，因此最佳深度的真实值应介于44~46 μm 之间;另一方面，从表格数据可看出，上下面积比对加工深度敏感，深度的微小变化即给面积比造成很大影响，也为进一步的区间细化带来难度。

　　表4 测量及计算结果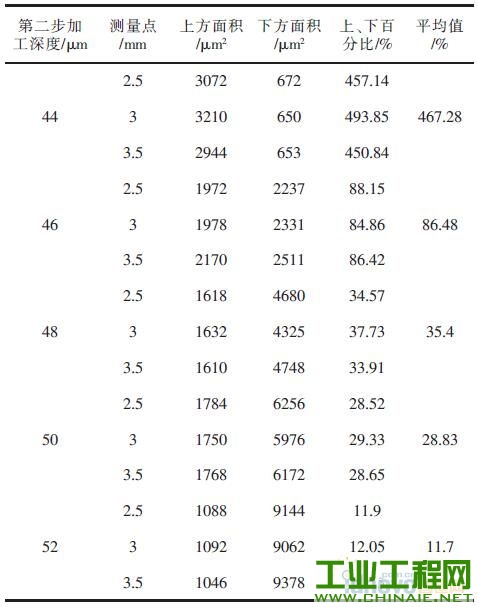

　　 5 、结论

　　(1)在采用定长补偿法的电火花铣削过程中，配合电极旋转，电极端面会形成圆锥形。

　　(2)利用定长补偿法加工三维型腔，会在一层加工后形成波浪状不平整表面，破坏了该方法初始加工表面为平面的模型。针对波浪面对加工底面的影响进行了仿真分析，结果表明波浪面对最终的型腔底面形状几乎不产生影响。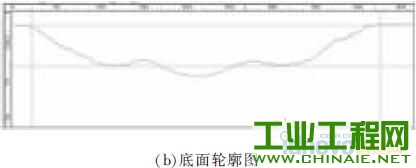

　　(3)为达到统计意义上的平面，确定了第二步加工的最佳深度的定义;并通过三角形假设和正弦曲线假设从几何上找到了最佳深度的取值范围。

　　(4)针对最佳深度值的获取进行了理论分析计算及实验探究， 结果表明当分层厚度为46 μm 时，上下面积最为接近，初定为最佳的分层厚度，而真实的最佳深度值介于44~46 μm 之间。