|
轨迹规划对工业机器人能够高效、稳定的运动有重要的影响。机器人工作时必须保证运行轨迹的平滑。若各关节的速度和加速度突变或者不连续会在机器人工作过程中,加剧机构的摩擦,机械臂出现振动现象,增大轨迹跟踪误差,降低跟踪精度,缩短机器人的使用寿命。为此学者们提出了多项式插值、B样条曲线插值等插值方法,从而得到关节速度和加速度平稳、光滑且连续的轨迹。 本文通过在MATLAB环境中仿真研究了三次多项式与五次多项式插值后,各关节的关节角度位置、速度和加速度的变化轨迹,通过研究分析提出了过路径点的点到点运动间的“353”∽1多项式插值,并且得到了关节速度和加速度的平滑连续的变化轨迹。 1.机器人运动学模型 本文以NACHI的六自由度MZ07工业机器人作为模型研究,确定机器人的连杆D—H坐标参数,如表1所示,在MATLAB中构建机器人的数学模型,如图1所示。 表1 MZ07机器人连杆D—H参数 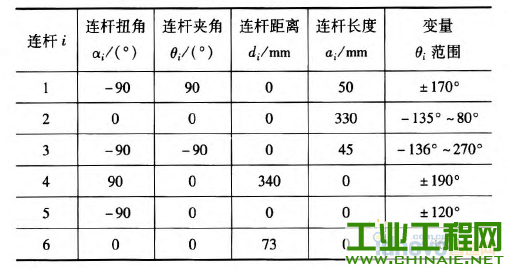  图1机器人MATLAB=维模型 2.关节空间轨迹插值研究 关节空间法是以含有关节角度的函数来描述机器人的轨迹,在进行关节空间轨迹规划时,需要通过运动学的逆解,将路径点转换成关节矢量角度值,再通过对每个关节拟合一个光滑函数,使从起始点开始,依次通过所有路径点,最后到达目标点。对于每段路径,每个关节运行时间均相同,则保证了所有关节同时到达路径点和目标点,此外,各个关节函数之间是相互独立存在的。采用关节空间法不需要在直角坐标系中描述两个路径点之间的路径形状,所以计算简单、容易,并且关节空间不会发生在直角坐标空间中的机构奇异性问题。 2.1过路径点的三次多项式插值 在单个关节运动过程中,为了使其能都平稳地运动,要求关节在起始点速度和目标点速度均要为0,而且关节起始角吼已知,终止点所可由运动学反解求得,则一个三次多项式可由起始点的关节角度、速度和终止点的关节角度、速度4个约束唯一确定。因此对三次多项式:  由上确定的三次多项式的系数可以代人式(1)、(2)中,分别可以得到单个关节此时刻的的关节角度、关节速度以及加速度。 但是在现实应用中,要求规划出过路径点的轨迹,然后在经过路径点时的机器人手臂末端状态会有两种情况:一种情况是机器人手臂由起始点运动到路径点时停留,即此时的在路径点处的速度为零,则可以直接使用前面的三次多项式插值算法;另一种情况是机器人手臂由起始点运动到路径点时不做停留,此时的速度已经不再为零,则该点再运动到目标点或者下一个路径点时,不能采用前面的三次多项式算法,故上式需要推广成为具有任意约束速度的三次多项式插值。在过路径点的轨迹中,可以把所有的路径点看做是“起始点”或者“目标点”,通过求解其逆解,得到各关节的关节矢量值,然后确定一个三次多项式插值函数,使各个路径点平滑地连接起来。只是此时的“起始点”与“目标点”处的速度不再为零。在确定此三次多项式的方法与前面所述方法相同,只是改变了速度约束,即:  对于各路径点处的关节速度,我们采用平均值法来确定,规定各路径点间的运动时间均相等,路径点速度可根据两侧的轨迹的角速度取平均值。如果对于运动轨迹的要求更加严格,则需要更高阶的多项式对运动轨迹进行插值。但不是阶数越高越好,高阶多项式轨迹会出现“龙格”现象。本文针对五次多项式进行研究。五次多项式可由6个约束唯一确定,即在起始点和目标点规定了关节位置、速度和加速度,从而来约束整个运动轨迹。五次多项式即:  2.3仿真研究 在MATLAB中对MZ07机器人的运动进行轨迹规划仿真,设有起始点A(一100,0,一300)、中间点曰(325,225,100)和目标点C(235,300,400)。从A点运动到B点用时1 s,从B点到c点用时1 S,求得三点的关节变量值,如表2所示。 表2轨迹点的关节角度 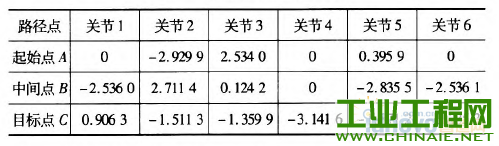 假定该运动的起始点与目标点的速度与加速度均为零。分别对该三点间的运动应用三次多项式插值和五次多项式插值,分别得到该过程中关节角度、速度和加速度的变化情况,如图2~7所示,三次多项式与五次多项式插值后的关节角度、角速度和角加速度的产生的最大值如表3所示。 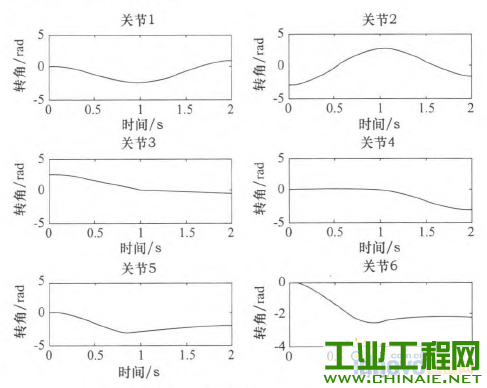 图2三次多项式规划后关节i一6角度位置 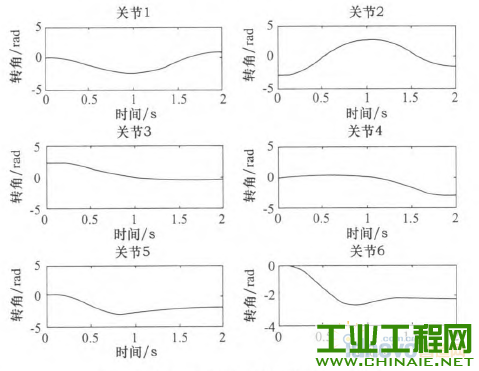 图3五次多项式规划后关节卜6角度位置 由仿真结果可知,三次和五次多项式都可以使运动轨迹平滑连续,但是三次多项式插值后,在关节加速度上出现突变,现实中机器人手臂在运动中很可能无法完成此运动过程。五次多项式的加速度虽然可以光滑地连续起来,但是最大角加速度达到-j'201.067 0rad/s2,使运行不够平稳缓和,也有害电动机的寿命。 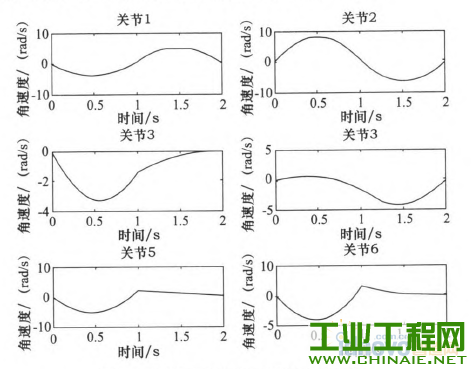 图4 三次多项式规划后关节1~6角速度 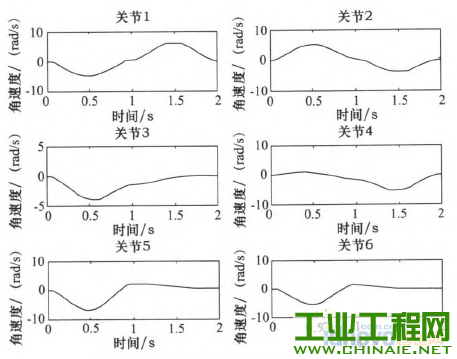 图5 五次多项式规划后关节1~6角速度 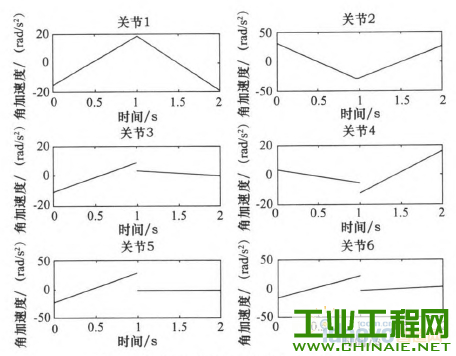 图6三次多项式规划后关节1-6角加速度 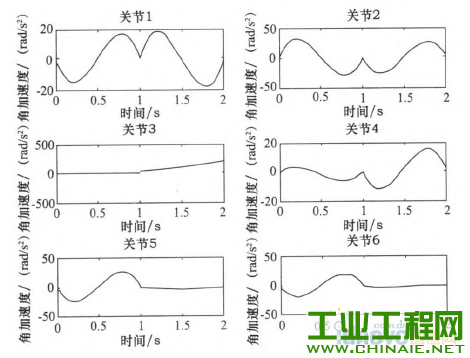 图7五次多项式规划后关节1~6角加速度 表3三次多项式与五次多项式最值比较 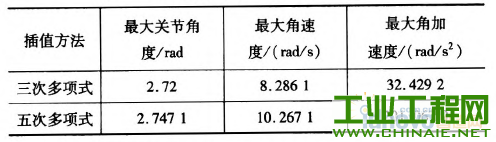 2.4过路径点的“353”[gj多项式插值。 在实际对机器人运动轨迹规划时,要求规划过路径点的轨迹,为了得到加速度合适且连续、平滑的变化轨迹,介于三次多项式和五次多项式的优缺点,采用了“353”一1多项式插值,即三次多项式与五次多项式结合的形式。如图8所示,该方法将整个轨迹分为3个阶段,第一阶段为在0一t。时间内采用三次多项式插值,第二阶段t。一t。时间内采用五次多项式插值,第三阶段t。一t,时间内采用三次多项式插值。本结构方法的要求,在两个相邻阶段的交点处的关节角度、角速度和角加速度要求相等。其中t。、t6可分别取0一t^、t^一f,时刻的中间时刻。 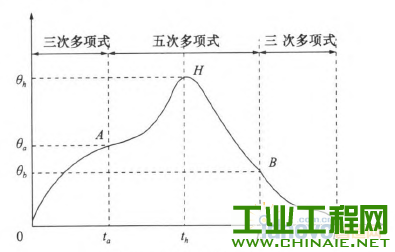 图8“353”多项式结构 同样使用2.3节假定的A、B、c三点。在MATLAB中仿真出“353”多项式结构算法规划后的各关节的关节角度、角速度和角加速度变化情况,如图9—10所示。规划后的关节角度、角速度和角加速度的最大值如表4所示。 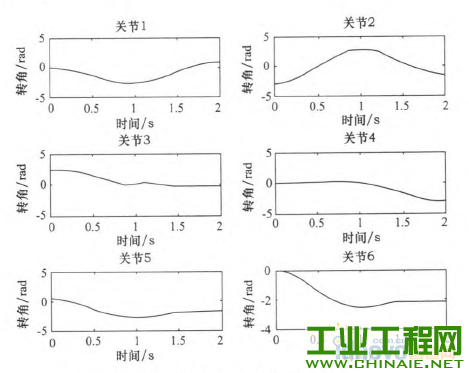 图9 "353”多项式关节角度 根据仿真结束所示,该方法可以得到平稳、连续的关节角度、角速度和角加速度的变化轨迹。与表3中的三次、五次多项式最大值比较,可以看出相对三次多项式可以得到平稳、连续的角加速度,同时相对五次多项式可以得到比较小的最大关节角加速度,从而使整个关节运动过程中更加平滑,减小了机构间的冲击。 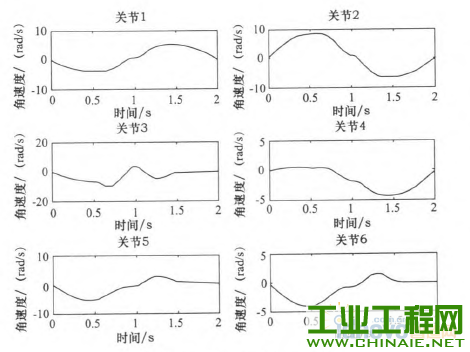 图10 “353”多项式关节角速度 表4“353”多项式最值 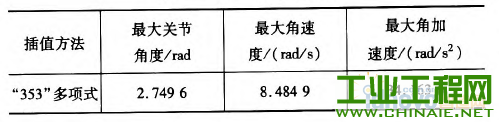 3.结语 本文通过在MATLAB环境中,基于MZ07工业机器人运动模型,分析了三次多项式和五次多项式的轨迹插值算法,对比了两个方法的优缺点。关节空间在“353”多项式插值规划后,通过仿真研究,“353”多项式插值既可以得到平稳、连续的角加速度轨迹,又可以得到较合适的最大角加速度,解决了三次多项式插值后关节角加速度不连续问题和五次多项式插值规划后关节最大角加速度较大问题。在关节空间中多项式插值的高低次结合使得各关节的变换优于单一使用的同次多项式插值。 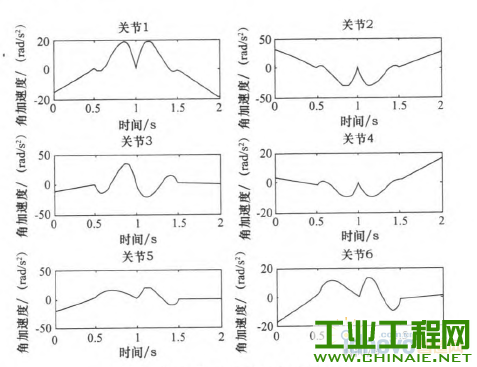 图11 “353”多项式关节角加速度 |
2020-02-17
2022-06-13
2021-12-13
2022-11-09
2022-10-20



 /1
/1 