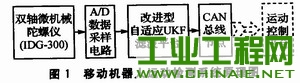
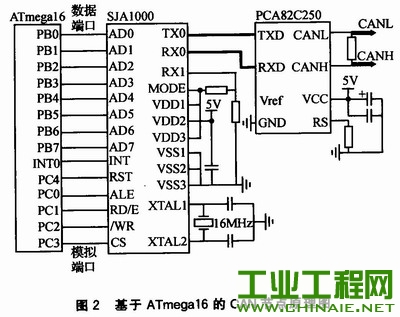
引言

　　在未知环境中，路况具有复杂性及未知性特点。移动机器人准确的路况探测及其自身的平稳运行，对机载设备与探测任务本身都非常重要。目前，对移动机器人运动控制研究多集中在前向通道的算法研究，有关状态信息检测、传输反馈环节的研究相对较少。

　　双轴微机械陀螺仪传感器可以测量机器人的俯仰与翻转，但微机械陀螺仪有随机漂移性，无法直接应用，需要对输出值作算法处理。参考文献中的微机械陀螺仪随机漂移的算法，可以在一定程度上解决漂移方面的问题，但仍有改进的空间，滤波性能有待进一步优化提高。在现有自适应UKF算法的基础上，改变比例对称采样策略的相关参数可达到较好的滤波效果。现有的以ATmegal6为微处理器的CAN总线程序还有一些不完备之处，本文采用PeliCAN模式加入了完备的错误分析程序，并支持系统自身测试功能。

　　1 系统硬件设计

　　移动机器人运动检测系统原理如图1所示。采用InvenSense公司生产的IDG300型双轴微机械陀螺仪进行移动机器人运动过程的俯仰与翻转角度检测;A/D采样电路的主芯片为8位A/D转换器ADC0809。采集的数据经改进的自适应UKF算法滤波后，经CAN节点向运动控制平台传输机器人的运动状态数据。以ATmegal6为微处理器，SJAl000为CAN协议控制器，PCA82C250为CAN收发器的CAN节点原理如图2所示。

　　2 系统软件设计

　　2.1 改进自适应UKF滤波算法

　　改进的自适应UKF算法如图3所示。

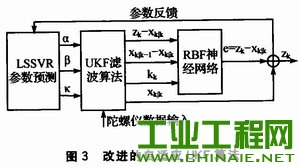　　经典UKF滤波算法采用某种策略得到状态估计sigma点集后，大致分两个步骤预测与更新，具体方程见参考文献。不同的采样策略会影响sigma点采样及sigma点个数计算。比例对称采样方法中具体的sigma点采样方法为：

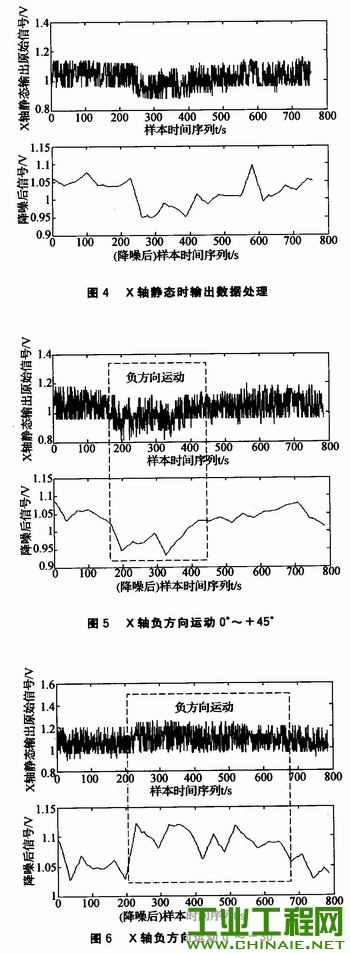
　　式(1)～式(5)中需要确定3个参数α、β和κ。有一定的经验值，但是微机械陀螺仪不同时间测量输出差别较大，固定的值不能满足角度测量的需要。在陀螺仪输出值有明显差别时，需要采用最小二乘支持向量回归机(LSSVR)对α、β和κ值进行回归，支持向量机对小样本的支持，因此可以做出下一步较准确的预测。结合参考文献中的算法原理，算法步骤如下：

　　①输入状态初始条件

　　②卡尔曼滤波估计的参数输入RBF神经网络，利用神经网络的自适应能力和函数逼近能力对这些特征量进行训练调整。

　　③更新方程。若输出角度输出较准确，则数据发往CAN总线，程序转至第②步。

　　④若输出角度有偏差，则LSSVR算法调整参数α、β、κ的值，程序转至第②步。

　　2.2 CAN节点程序设计

　　以ATmegal6作CAN节点的微处理器需要解决端口(ALE，RD/E，/WR)的模拟问题。CAN节点部分主从机，节点ID地址决定是否接收任务以及发送的顺序;帧格式采用数据帧;帧类型采用扩展帧;PB0～PB7作地址数据总线;PC3输出片选信号;PC4控制SJAl000的复位引脚;INT0(PD2)控制终端信号。错误检测分析程序包括：仲裁丢失捕捉(ALE)、错误代码捕捉(ECC)、错误警告限制(EWLR)、RX错误计数(RXERR)、TX错误计数(TXERR)寄存器配置。

　　程序流程如下：

　　①SJAl000寄存器地址配置;

　　②CAN初始化、进入复位状态配置时钟分频、代码验收、验收屏蔽寄存器。

　　③等待总线数据，判别报文是否有效：若有效，进入收发函数，发送完毕转至第③步;若报文无效，则进行错误处理，程序转至下一步;

　　④错误分析，丢掉错误报文。程序转至第③步。

　　3 实验分析

　　3.1 数据来源

　　实验条件：陀螺仪测试系统一套(包括360个脉冲/圈的编码器、IDG-300软硬件系统)，使用Matlab仿真平台。测试系统可以在±50°摆动运动，陀螺仪的偏转角度通过编码器输出，精度为1°。

　　3.2 陀螺仪数据处理

　　所有数据通过测试系统实验获得。篇幅有限，下面给出X轴输出数据采用改进自适应UKF算法后的滤波效果，如图4～图6所示。从图中可以看出，该方法明显缩成了数据波动范围。

　　3.3 CAN总线数据传输

　　对CAN总线数据传输稳定性做了相应实验。取数量相同的数据，分别通过总线和串口进行传输，信号线长度都是2 m，分别进行相同数据量的1 h和24 h数据传输实验。实验结果如表1所列。

　　CAN总线通信方式是指在两个节点间通信;串口通信是指使用ATmegal6芯片的RXD、TXD引脚功能进行数据传输。正确率的计算方法为：通信正确率=正确接收数量个数/发送数据总个数。

　　结语

　　通过改进自适应UKF滤波算法处理新型双轴微机械陀螺仪数据，使微机械陀螺仪输出数据相对稳定，一定程度上降低了微机械陀螺仪随机漂移。数据传输采用CAN总线通信的方式，提高了数据传输的正确率与稳定性。

　　但该系统尚不完善，特别是处理微陀螺仪随机漂移问题的方法有待进一步改进，以提高微机械陀螺仪的精度，使机器人运动检测更精确。