|
0.前言 不论是串联机器人还是并联机器人,在现有条件下还无法对机器人的末端位姿进行实时和直接的测量。现有的一般方法是利用机器人的机构关节参数和运动学模型通过计算来间接地获得。因此机器人的末端位姿精度在很大程度上取决于机器人的关节参数的标定精度。机器人由于结构特征、安装位姿等因素的影响,现场直接测量所得到的机构参数往往不够准确,直接导致了机器人末端位姿精度的降低。因此,机器人机构参数的获取即机器人的运动学标定问题是机器人高精度定位控制的基础和核心问题,同时也是机器人领域的难点问题之一。机器人的运动学标定~直是机器人学研究领域的一项重要内容,国内外学者针对标定问题做了大量研究工作。SUN等u1提出了一种新的基于闭环矢量法的误差源分类方法,将几何误差源分为补偿误差和非补偿误差两种,为误差的标定、补偿提供了帮助。VERL等根据辨识矩阵条件数确定了测量构型的选取方法,研究了测量构型的选取数量与末端位姿误差之间的关系。为了提高了标定效率,REN等p1提出通过安装双轴倾角仪来调节运动平台的姿态,在姿态约束的情况下选取有效测量构型进行运动学标定,并利用仿真和试验验证了这种方法的有效性。BAI等【41则提出一种模糊差值标定方法,不仅简化了标定过程,而且适合并联机器人工作空间较小的特点。ZHANG等15-6]提出一种并联机器人误差综合补偿方法,基于虚拟误差理论将几何误差、热误差等假设成单一的虚拟误差源,利用共存演化神经网络算法对虚拟误差实现了补偿。 近年来,粒子群优化算法(Particle swarmoptimization,PSO)已经被逐步地应用于机器人运动精度、路径规划等领域的相关研究中。特别是量子粒子群优化算法(Quantum—behaved particle swarmoptimization,QPSO),以量子物理基本理论为基,与粒子群优化算法相比具有更好的全局搜索能力,更适合机器人学研究中的多参数组合优化问题。黄进等p1利用PSO算法对外部轴内关键参数进行优化,试验表明机器人与外部轴系统的整体精度有了较大的提高。谢平等ll叫利用PSO算法对并联机器人驱动杆杆长参数进行优化,有效地修正了期望轨迹与理想轨迹之间的偏差。LI等【lu将神经网络与PSO算法相结合,对并联机器人的运动学正解进行求解,仿真结果显示该方法能够达到并联机器人在线控制所需的运算速度与求解精度。JUANG等llzJ基于PSO算法与递归神经网络两种算法提出一种新的机器人动力学步态学习方法,并在一款hexapod型机器人的步态控制器上成功使用。COUCEIR等u纠将PSO算法应用于多机器人系统的研究中,在仿真与试验环境下实现了多机器人的避障功能。史也掣141提出了一种基于QPSO算法的路径规划方法,通过规划空间机器人机械臂关节角的运动,使得基座姿态和机械臂末端姿态能够同时到达期望状态。 本文在上述研究的基础上,提出一种同样适用于串联、并联机器人的运动学标定方法。首先,对典型的串联机器人、并联机器人分别进行运动学分析,建立包含铰链中心位置误差、转动轴线偏转误差、杆件长度误差等误差源的误差模型,将模型内的误差源作为相应的机构参数修正量。然后,将机器人的运动学标定问题转化为非线性系统的优化问题,以机构参数的修正量作为优化变量,以机器人位姿精度要求设计目标函数,基于位姿误差模型建立一个多参数的非线性优化系统。最后,利用量子粒子群优化算法对目标函数进行计算,根据获得的机构参数修正量更新运动学模型,实现对机器人机构参数的标定。 需要指出的是,影响机构参数的误差因素有很多,包括随机误差和系统误差等。本文方法只是针对关节误差中的系统误差进行求解标定,不适用于间隙等典型的随机误差。 1.机器人机构参数标定流程 并联机器人和串联机器人的运动学求解具有不同的特点,本文利用并联机器人的逆运动学方程和串联机器人的正运动学方程来建立相应的标定模型。 并联机器人的标定流程如图1所示:①利用逆运动学方程建立机器人的位姿误差模型;②根据测量和标定的需求选择适当的构型及相应的理想位姿上L;③利用逆运动学方程计算理想情况下对应的机构参数知:④基于实际测量得到的末端位姿误差e,利用量子粒子群算法进行寻优,计算机构参数修正量却;⑤将机构参数修正量却与理想机构参数g。相加得到最优机构参数g,作为并联机器人运动学标定的结果。 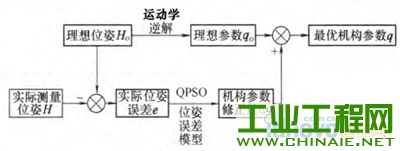 图l并联机器人标定流程 串联机器人的标定流程如图2所示:①利用正运动学方程建立机器人的位姿误差模型;②根据测量和标定的需求选择合适的理想机构参数劬;③利用正运动学模型计算理想情况下对应的末端位姿玩;④根据实际测量得到的末端位姿误差e,利用量子粒子群算法进行寻优,得到机构参数修正量幻;⑤将机构参数修正量却与理想机构参数铷相加得到最优机构参数g,作为串联机器人运动学标定的结果。 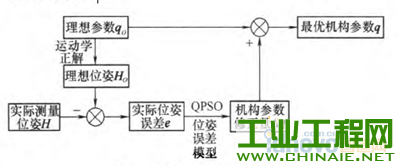 图2串联机器人标定流程 2.量子粒子群优化算法的基本原理 量子粒子群优化算法,由Ⅳ个代表潜在问题解的粒子组成群体,在一个M维的目标搜索空间内进行搜索。在t时刻,第f个粒子的位置为   3.机器人位姿误差建模 分别选用比较典型的Stewart并联机器人、Puma560串联关节型机器人作为机器人运动学模型的建模对象,建立机器人内主要误差源与末端位姿误差之间的关系。 3.1并联机器人位姿误差模型  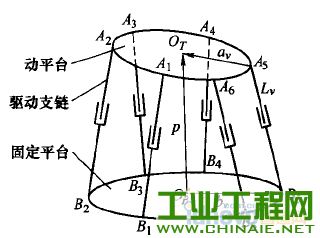   3.2 串联机器人位姿误差模型  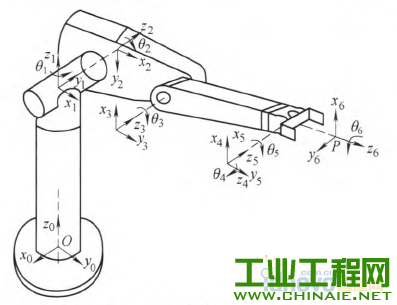 图4 Puma560串联机器人结构简图    4.基于量子粒子群优化算法的标定问题求解 将标定问题转化为非线性系统的最优化问题,利用量子粒子群优化算法进行求解。 4.1确定优化变量 确定机构参数修正量△g为最优化问题求解的目标变量。由运动学方程式(8)与式(10)可以看出,通过调整机器人误差模型中的各类误差源可以影响机器人的末端位姿。将模型内误差源作为相应的机构参数修正量却,利用优化算法寻找一组最优的修正量衄就可以实现机器人机构参数的标定。另外,由于本文研究重点在于机器人机构参数的标定,所以对驱动杆的控制误差不予考虑。因此,将机构参数修正量幻确定为最优化问题的优化变量。对于求解最优化问题的量子粒子群优化算法,每个粒子都代表一组用于优化机器人机构参数的解,其位置矢量X(幻就是最优化问题的优化变量,即机构参数修正量却。   4.3量子粒子群优化算法的计算步骤 设粒子数为Ⅳ,迭代次数用t表示,最大迭代次数为‰。。利用量子粒子群优化算法计算标定问题的具体流程如下。 (1)在机器人工作空间内选取肛组构型进行测量,得到相应的实际测量位姿日,通过计算得到实际位姿误差eh,h=1,2,...,μ。 (2)初始化粒子群算法相关参数。置t=O,根据式(1),随机初始化Ⅳ个粒子的初始位置X(0),粒子位置矢量的维数M等于相应类型机器人机构参数修正量△口的维数。   (5)根据量子粒子群优化算法,利用式(2)~(4)分别计算粒子群的平均最优位置aD以及每个粒子的随机点位置p,,更新每个粒子的位置矢量Xi(T+1)。 (6)判断是否满足迭代算法的终止条件,即机器人运动精度要求。如果满足,粒子群的全局最优位置Pg(t)就是机器人运动学标定问题的最优解△q,将其与理想机构参数q0。相加就能得到标定后的最优机构参数q;若未满足终止条件,返回步骤(3)继续计算。另外,当t=tmax,计算结束。 5.五轴并联机床试验分析 5.1五轴并联机床结构简介 五轴并联机床结构图如图5所示,该机构由固定平台、工作平台、动平台、平面约束机构、四个驱动分支构成。五轴并联机床采用高刚度且力流封闭的龙门结构。固定在两侧立柱顶端的四个伺服电动机分别驱动四组滚珠丝杠副,滚珠螺母(滑块)通过四根支杆与动平台相连,通过调整滑块的位移来实现动平台的运动。在固定平台、动平台之间j由四块板件组成了平面约束机构,约束机构部分内各转动轴线与工作台运动方向平行。 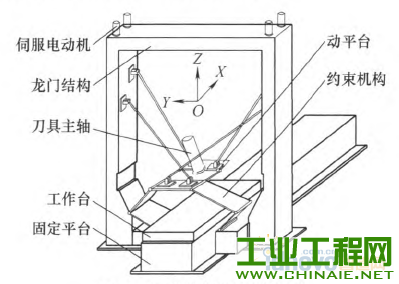 图5五轴并联机床结构图 5.2约束机构部分误差模型 根据约束机构部分的结构特征及其平面运动的特性,将平面约束机构、动平台以及工作台综合简化为六杆串联机构(图6)。如果各转动副轴线问的平行度误差较大,严重时甚至会影响到约束机构部分运动自由度的数量,所以机构内安装的转动副具有较高的精度水平。假设铰链间隙以及轴线间的平行度误差较小,可以忽略。因此,平面约束机构内的几何误差源主要包括工作台姿态误差以及各杆件的长度误差。 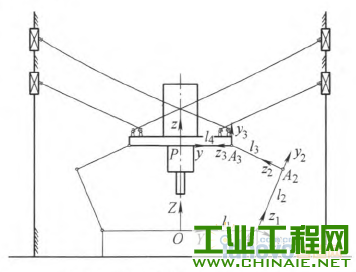 图6 五轴并联机床原理简图 经过上述分析,将约束机构部分内主要误差源转化为机构参数修正量却,经整理如表1所示。其中,工作台的姿态误差被分为绕Y轴与绕Z轴的偏转修正量。 表1约束机构部分机构参数修正量  然后,根据约束机构部分结构参数的设计值,依次沿转动副Al、A2、A3,建立由基坐标系D系到动坐标系JP系的理想位姿方程  这样即可得到约束机构部分的运动学模型,建立起各项机构参数修正量与末端位姿误差之间的联系。 5.3基于量子粒子群优化算法的标定试验 通过调整模型内各参数修正量可以对动平台各个方向上的位置误差产生影响,而作为机床驱动部分的并联机构部分能够对其中y轴、z轴方向上的位置误差进行补偿。因此,在针对五轴并联机床约束机构部分进行的运动学标定试验中,利用工作台运动Ⅸ轴)方向上的精度要求建立优化目标函数,对约束机构部分的机构参数进行标定。  表2 x轴向末端位置误差测量结果 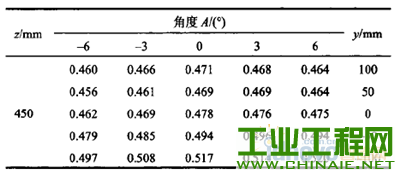  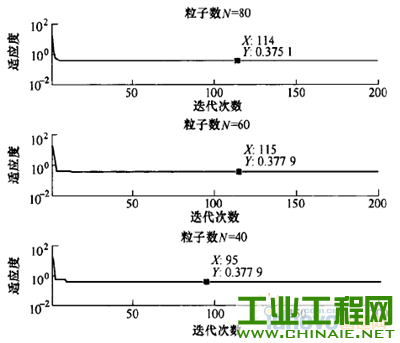 图7迭代计算结果 结果表明,粒子数对于QPSO算法的收敛效果影响较小,当粒子数由60增加到80时,最小适应度从0.377 9减小到0.375 1,标定效果的提高程度较小,但同时降低了效率。当粒子数为40时,仅用95次迭代就获得了相同的最小适应度0.377 9,表明了QPSO算法具有一定的随机性。取粒子数N--60的迭代计算结果,获得机构参数修正量的优化结果,如表3所示。 表3机构参数修正量  将修正量引入约束机构部分的运动学模型,得到优化后的x轴向末端位置误差(表4)。结果中显示优化后最大误差为0.019 3 mill,最小误差为0.0001 mlil,平均误差约为0.007 5 mill,经过参数优化后,X轴向的位置精度有了明显改善。 表4优化后的X轴向末端位置误差 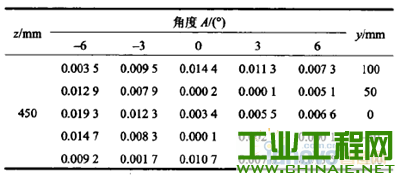 利用模糊差值标定方法对Stewart并联机器人进行了运动学标定,标定后在10 rrlrnx 10lain×10 IIllll的立方体空间内,最大位置误差为0.049 5 rain,平均误差为0.001 1 min;在20mmx20minx20 mill的空间内,最大位置误差为0.091 2 mm,平均误差为0.010 8 mnl。与模糊差值标定结果相比,基于量子粒子群优化算法的标定方法能够在更大的工作空间内实现运动学参数的有效标定;而且最大末端位置误差为0.019 3 rain,标定效果的均匀性更好。 6.结论 (1)针对并联、串联两类机器人进行误差建模,分析标定流程,基于量子粒子群优化算法,提出了一种适用于并联机器人与串联机器人的标定方法,能够实现机器人关节变量和其他关节参数的有效辨识。 (2)机器人关节结构较为复杂,完成装配后对机构关节参数直接进行测量标定的难度较大。利用量子粒子群优化算法具有全局优化能力的特点,对非线性运动学模型中的机构参数进行优化,可以将复杂的运动学标定问题简单化。 (3)以五轴并联机床的约束机构部分为例,利用实测数据获得的标定结果表明了基于量子粒子群优化算法的标定方法是一种快速的、能够有效改善精度的标定方法。 |
2020-02-17
2022-06-13
2021-12-13
2022-10-20
2022-11-09


 /1
/1 